Кожинин Сергей Павлович
О гравитационном смещении частоты света
и замедлении времени
В статье рассматриваются задачи о распространении света в гравитационных
полях. Результаты, полученные при решении задач, имеют фундаментальный
характер и дают информацию об эффекте гравитационного смещения частоты
света и эффекте замедления времени. Задачи решаются в рамках ньютоновской
теории тяготения и квантовой теории света. Обсуждаются пределы применимости
ньютоновской теории тяготения.
Рассматриваемые в статье задачи входят в авторский практикум
"физика и астрофизика в задачах и упражнениях" и предлагаются ученикам
классов с углубленным изучением физики, математики, астрономии.
Предполагается, что школьники имеют четкие представления об эффекте
Доплера, доплеровском смещении частоты (длины волны) спектральных линий и
имеют опыт решения задач по этой теме (см. [1.- пар.53, Упр.53], [2.-пар.24],
[З.-пар.23]).
Задачи, предлагаемые в статье, являются базовыми, т.е. эти задачи дают
минимальный уровень ЗУН (знаний, умений, навыков), необходимый для решения
более сложных задач и понимания ряда фундаментальных вопросов современной
физики и астрономии, например: практические применения эффекта Мессбауэра,
спектры космических объектов, элементы общей теории относительности
А.Эйнштейна и элементы релятивистской астрономии.
В статье приводятся комментарии, в которых дается краткая информация об
эффектах гравитационного смещения частоты и замедления времени в общей теории
относительности А.Эйнштейна. Рассматриваются сильные эффекты в поле тяготения
черной дыры Шварцшильда.
Задача 1.
Фотон частоты ω0 испущен из точки,
находящейся на высоте Н0 над поверхностью Земли.
1)Какой будет частота фотона ω на высоте Н? Рассмотреть два случая:
а) Н>Н0;
б) Н<Н0. Считать, что Н0<<R
и H<<R, где R - радиус Земли (приближение однородного поля тяготения).
2) Найти относительное изменение частоты фотона
Δω/ω0o=(ω-ω0)/ω0
(параметр гравитационного смещения частоты) в однородном поле тяготения.
Численный ответ получить для случая, когда разность высот составляет
|ΔН|=20 м.
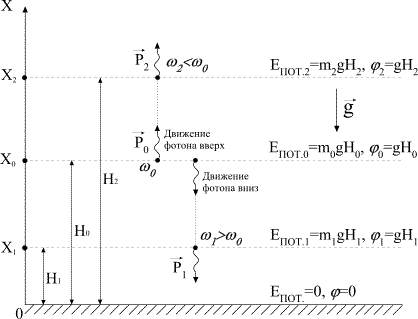
Рис.1.
В задаче рассматривается движение фотона в однородном поле тяготения, когда
напряженность гравитационного поля (ускорение свободного падения) g не зависит
от высоты Н. По закону сохранения энергии, полная энергия фотона, равная сумме
его энергии
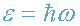
и потенциальной энергии Е
ПОТ,
есть величина постоянная, т.е.
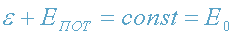 , (1)
, (1)
где Е - полная энергия в начальный момент (определяется из начальных условий).
В однородном поле тяготения потенциальная энергия частицы массы m определяется
формулой Е
ПОТ=mgx (потенциальная энергия "нормирована на ноль" в точке x=0
выбранной системы отсчета). В данной задаче систему отсчета удобно связать с
поверхностью Земли и ось координат ОХ направить вертикально вверх (рис.1).
При таком выборе системы отсчета x=Н. Теперь перепишем уравнение энергии (1)
в виде
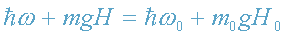 . (2)
. (2)
Т.к. масса фотона
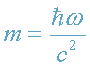
, то из (2) получаем:
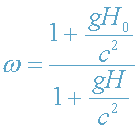 . (3)
. (3)
Эту формулу можно упростить, если учесть, что
gH/c
2=(GM/Rc
2)H/R=7*10
-10<<1
(здесь G=6,67*10
-11 Нм
2/кг
2
- гравитационная постоянная, М=6*10
24 кг, R=6,4*10
6 м - масса и радиус
Земли соответственно). Учитывая теперь, что
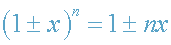
при x<<1 и пренебрегая величинами второго порядка малости
(gH
0*gH/c
4->0), формулу (3) приводим к виду
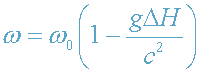 , (4)
, (4)
где ΔН=Н-Н
0. Очевидно, что относительное гравитационное смещение
частоты (параметр гравитационного смещения) определяется формулой
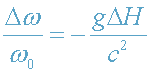 . (5)
. (5)
Из полученных результатов (4)-(5) следует:
1) Если фотон удаляется от Земли (ΔН>0), то Δω<0, т.е.
частота фотона уменьшается, - гравитационное красное смещение.
2) Если фотон приближается к Земле (ΔН<0), то Δω>0, т.е.
частота фотона увеличивается, - гравитационное фиолетовое смещение.
3) При |ΔH|=20 м Δω=2*IO-15. Столь малое гравитационное
смещение частоты удалось обнаружить экспериментально в I960 году с помощью
эффекта Мессбауэра в опытах Паунда и Ребки.
Заметим, что формулы (4)-(5) можно выразить через разность потенциалов поля
между точками испускания и приема фотона. Потенциал поля - это скалярная
(энергетическая!) характеристика поля. Потенциал гравитационного поля
определяется отношением потенциальной энергии частицы в данном поле к ее массе:
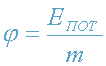 . (6)
. (6)
Очевидно, что потенциал однородного поля тяготения в точке X (на высоте Н)
равен
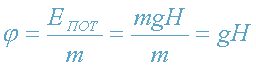 . (7)
. (7)
С учетом (7) формулы (4)-(5) принимают вид:
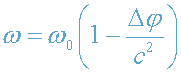 ,
,
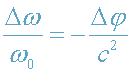 , (8)
, (8)
где Δφ=φ
H-φ
0=gΔH,
φ
H=gH и φ
0=gH
0 - потенциалы поля в точке наблюдения (на высоте Н) и
в точке испускания (на высоте Н
0) фотона соответственно.
Эту задачу можно решить и другим способом. Т.к. при движении фотона в
гравитационном поле его частота изменяется, то изменяется и его масса
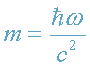
. Запишем уравнение движения частицы с переменной массой:
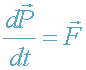
, где
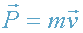
- импульс частицы, движущейся в поле силы
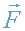
[1-c.237].
При
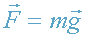
, где
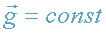
(постоянное однородное поле тяготения), имеем:
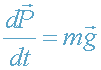
,
или в проекциях на ось координат ОХ (рис.1)
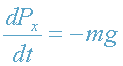 . (9)
. (9)
где P
x=mv
x. Для определенности будем считать, что частица движется вертикально
вверх, т.е. вдоль положительного направления оси ОХ. Тогда P
x=mv.
Т.к. импульс фотона P=mc, где c=const, то уравнение движения (9) принимает
вид
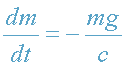
. Разделяя переменные m и t, запишем:
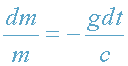
. Т.к. масса фотона
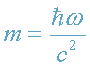
и dx=cdt, то последнее уравнение приводим к виду
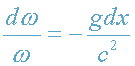
. Интегрируя, получаем:
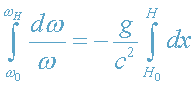 ,
,
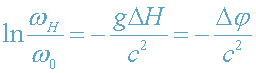 ,
,
где ω
0 и ω
H - частота испущенного (на высоте Н
0) и частота
наблюдаемого (на высоте Н) фотона соответственно, ΔН=Н-H
0,
Δφ=φ
H-φ
0=gΔH.
Очевидно, что частота фотона ω
H равна
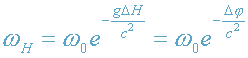 . (10)
. (10)
Как видим, частота фотона изменяется по экспоненциальному закону:
возрастает при ΔН<0 и убывает при ΔН>0. Далее, учитывая,
что
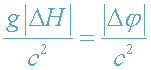
, формулу (10) приводим к виду (4) (или (8)).
При этом надо учесть, что
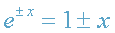
при х<<1.
Задача 2.
Фотон частоты ω0 испущен с поверхности звезды, масса которой
равна М и радиус R.
1. Найти частоту ω и параметр гравитационного смещения частоты
Δω/ω0 фотона на расстоянии r от центра звезды (рис.2).
2. Какими будут результаты для бесконечно удаленного от звезды
наблюдателя? Численный ответ получить при М=МC=2,0*1030 кг.
R=RC=7,0*108 м (масса и радиус Солнца).
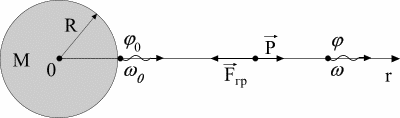
Рис.2. |
С поверхности звезды с потенциалом φ0=-GM/R
испускается фотон
частоты ω0. Наблюдатель, находящийся в точке с гравитационным
потенциалом φ=-GM/r на расстоянии r от центра звезды,
регистрирует фотон
частоты ω. 0r - радиальная ось координат системы отсчета, связанной с
центром звезды. Fгр - сила гравитации, действующая на фотон.
|
Потенциальная энергия частицы массы m в ньютоновском неоднородном поле
тяготения центрального тела массы М и радиуса R (планеты или звезды)
определяется формулой
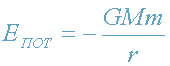
,
где
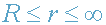
(потенциальная энергия "нормирована на
ноль" в бесконечности). Соответственно, потенциал поля (6) в данной точке
пространства определяется формулой
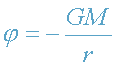
.
Очевидно, что E
ПОТ=mφ. Закон
сохранения энергии фотона (1) запишем в виде
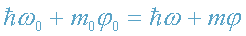 . (11)
. (11)
где
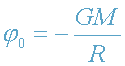
- потенциал поля на поверхности звезды
(в месте испускания фотона),
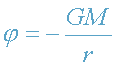
- потенциал поля на расстоянии r от центра звезды
(в месте наблюдения фотона). Учитывая, что масса фотона
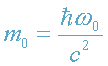
(в месте испускания) и
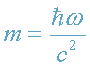
(в месте наблюдения),
уравнение (11) перепишем в виде
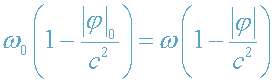 , (12)
, (12)
где
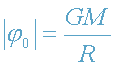
и
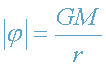
.
Из (12) получаем:
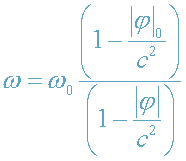 . (13)
. (13)
Легко убедиться в том, что для обычных небесных тел выполняется сильное
неравенство
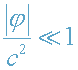 , (14)
, (14)
т.е. поля тяготения обычных планет и звезд являются слабыми (условие
(14) называют приближением слабого поля). Например, для Солнца
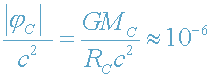
.
В приближении слабого поля (14) формулу (13) приводим к виду
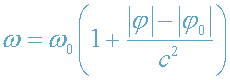 , (15)
, (15)
(учли, что (1+-x)
n=1+-nx при х<<1 и пренебрегли величиной второго порядка малости
|φ|*|φ|
0/c
4. Очевидно, что параметр гравитационного смещения частоты -
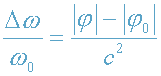 . (16)
. (16)
Для бесконечно удаленного наблюдателя (
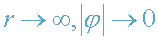
)
формулы (15) - (16) принимают вид:
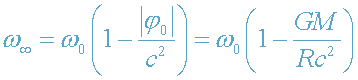 , (17)
, (17)
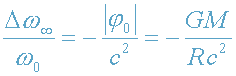 . (18)
. (18)
При M=M
C и R=R
C получаем:
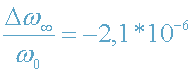
.
На основании полученных результатов (15) - (18) можем сделать следующие выводы:
1. Если |φ|>|φ|0, то ω>ω0, - фиолетовое смещение.
Если |φ|<|φ|0, то ω<ω0, - красное смещение.
Таким образом, частота света возрастает с увеличением абсолютной величины потенциала гравитационного
поля, т.е. при приближении к создающим поле телам; наоборот, при удалении от этих тел частота
света уменьшается.
2. Линейчатый спектр, испускаемый какими-либо атомами, находящимися, например,
на Солнце, выглядит там точно также, как выглядит на Земле спектр, испускаемый
находящимися на ней такими же атомами.
Если же на Земле наблюдается спектр,
испускаемый атомами, находящимися на Солнце, то его спектральные линии
окажутся смещенными по сравнению с линиями такого же спектра, испускаемого на
Земле: каждая линия с частотой ω0 будет смещена на интервал Δω,
определяемый из формулы (15)-(16):
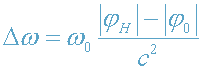 , (19)
, (19)
где φ
0 и φ
H - потенциалы гравитационного поля соответственно в месте
испускания и в месте наблюдения спектра. Если |φ
H|<<|φ
0| (для системы
"Солнце - Земля" это условие выполняется. - см. задачу 3), то формулу (19)
можно записать в виде
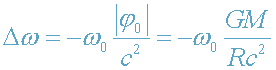 , (20)
, (20)
что соответствует приближению бесконечно удаленного наблюдателя (см.(17)-(18)).
Учитывая важность полученных результатов, решим задачу другим способом
(см. второй способ решения задачи 1). Понятно, что масса фотона при движении в
гравитационном поле изменяется. Запишем уравнение движения фотона, удаляющегося
от звезды в радиальном направлении OR (рис.2):
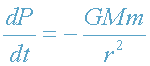
или,
т.к.
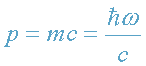
, то
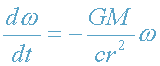
. Умножив обе части этого уравнения на dr=cdt
и разделяя переменные ω и r, получаем:
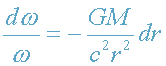 .
.
Интегрирование этого уравнения дает результат:
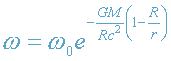 . (21)
. (21)
Соответственно, параметр гравитационного смещения частоты -
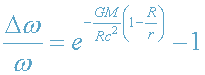 . (22)
. (22)
В приближении слабого поля (14) формулы (21)-(22) приводятся к виду (15)-(16).
Задача 3.
Фотон частоты ω0 испущен с поверхности Солнца. Вычислить
параметр гравитационного смещения Δω/ω0 спектральных линий частоты
ω0 спектра, наблюдаемого на Земле.
Масса Солнца MC=2,2*1030 кг,
его радиус RC=7,0*108м. Масса Земли Мз=6,0*1024 кг, ее радиус
Rз=6,4*106 м. Расстояние от 3eмли до Солнца α=1 а.е.=1.5*1011 м.
В этой задаче рассматривается движение фотона в неоднородном поле тяготения
двух тел - Солнца и Земли. Закон сохранения энергии (1) для фотона запишем в
виде (см. задачу 2)
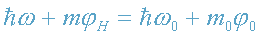
,
где φ
0 и φ
H - потенциал гравитационного
поля Солнца и Земли в месте испускания и в месте приема фотона соответственно:
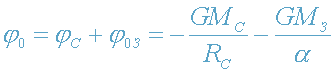 ,
,
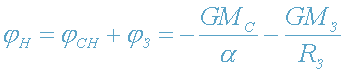
(принцип суперпозиции полей) . Из закона сохранения энергии фотона получаем:
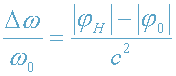 . (23)
. (23)
где |φ
0|=|φ
0З|+|φ
C|,
|φ
H|=|φ
З|+|φ
CH|. Далее получаем:
|φ
0З|=2,7*10
3(м/с)
2,
|φ
C|=1,9*10
11(м/с)
2,
|φ
З|=6,3*10
7(м/с)
2,
|φ
CH|=8,9*10
8(м/с)
2.
Таким образом, параметр гравитационного смещения частоты в спектре Солнца
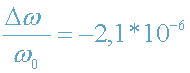
(см. также задачу 2).
Т.к.
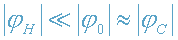
, то для Солнца и тем более для других,
более удаленных звезд, спектры которых наблюдаются на Земле, формулу (23) можно
записать в виде
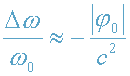
где φ
0=-GM/R - потенциал поля на поверхности звезды массы М и радиуса R.
Задача 4.
В данном месте частота фотона зависит только от свойств испускающих
их атомов (или ядер). На этих свойствах основано измерение хода времени в
данном месте (атомные часы). Поэтому наблюдатель, находящийся в точке с
другим гравитационным потенциалом, будет интерпретировать гравитационный
сдвиг частоты как изменение хода времени.
Пусть Δτ - промежуток времени между двумя сигналами, которые
испускаются с поверхности звезды массы М и радиуса R,
а
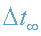
- промежуток
времени между этими же сигналами, регистрируемыми бесконечно удаленным
наблюдателем. Сравнить эти промежутки времени.
Если с поверхности звезды испущен электромагнитный сигнал частоты ω
0,
то бесконечно удаленный наблюдатель регистрирует сигнал, частота которого
определяется формулой (17):
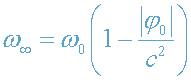 .
.
Под промежутками времени Δτ и
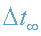
можно подразумевать периоды электромагнитного сигнала:
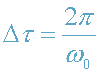
и
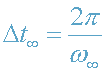
.
Тогда связь между Δτ и Δt имеет вид:
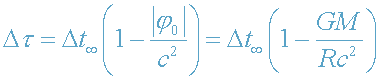 . (24)
. (24)
Как видим, Δτ <
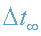
,
т.е.
время на поверхности звезды течет медленнее,
чем для удаленного наблюдателя, причем чем больше абсолютная величина
гравитационного потенциала на поверхности звезды |φ0|, тем медленнее там
течет время!
Комментарии.
Рассмотренные в задачах 1-4 эффекты смещения частоты и замедления времени в
гравитационном поле являются "близкими родственниками". Эти эффекты были
предсказаны и описаны в рамках общей теории относительности ОТО А.Эйнштейна.
В предельном случае слабых гравитационных полей (14) результаты ОТО совпадают
с результатами классической (ньютоновской) теории гравитационного поля
(принцип соответствия).
Рассмотрим сферически-симметричное поле тяготения звезды массы М и радиуса R,
находящейся в вакууме. Решение уравнений Эйнштейна для этого случая было
найдено Шварцшильдом (1916 г.). Остановимся на некоторых результатах этого
решения, имеющих прямое отношение к нашим задачам 2-4.
1. Замедление времени и гравитационное смещение частоты света в ОТО.
Из уравнений ОТО следует, что
физическое время τ, текущее в данной точке
пространства, находящейся на расстоянии r от центра звезды, определяется
формулой [4.-C.322]
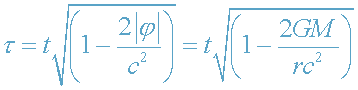 , (25)
, (25)
где
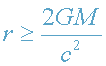
(внешнее решение Шварцшильда).
Радиус
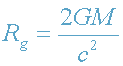
называется
радиусом Шварцшильда
или
гравитационным радиусом, а сфера с радиусом R
g -
сферой
Шварцшильда. Для обычных небесных тел R>>R
g.
Физическое время τ, текущее в данной точке r пространства, называют также
собственным временем. Время t в формуле (25) называют мировым или
координатным временем. Смысл мирового времени t в постоянном поле тяготения
(сферически-симметричное поле Шварцшильда является постоянным) заключается в
том, что его промежуток между двумя событиями в некоторой точке пространства
совпадает с его промежутком между любыми другими двумя событиями в любой
другой точке пространства, соответственно одновременными с первой парой
событий. Но одинаковым промежуткам мирового времени t соответствуют в разных
точках пространства различные промежутки собственного времени τ!
Из (25) следует, что вдали от центра тяготения (при

)
τ=t, т.е. t - это физическое время наблюдателя на бесконечности.
При меньших r время τ течет
все медленнее по сравнению со временем на бесконечности. При r=R
|φ|=|φ
0|=GM/R формула (25) принимает вид
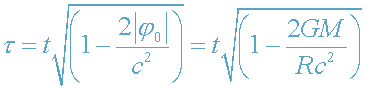 . (26)
. (26)
Для обычных небесных тел |φ
0|/c
2=GM/Rc
2<<1,
т.е. поле тяготения является ньютоновским. В этом случае формула (26) принимает вид
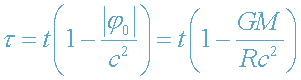 ,
,
что совпадает с формулой (24).
Теперь рассмотрим изменение частоты фотона при движении вдоль радиальной
линии Or. Пусть в некоторой точке с r=r
1 происходят вспышки с интервалом
Δt, измеренным в мировом времени. Т.к. поле статично, то эти вспышки
придут к наблюдателю в точку r=r
2 с тем же интервалом Δt. Интервалы
собственного времени в этих двух точках (см.(25))
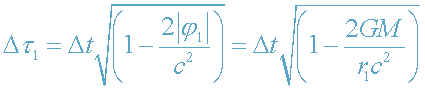 ,
,
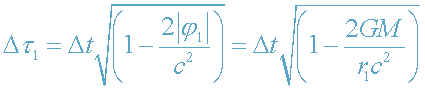 .
.
Т.к. частота, измеренная в собственном времени, равна
ω=2π/Δτ,
то ω
1/ω
2=Δτ
2/Δτ
1.
Следовательно, в точке наблюдения частота фотона равна
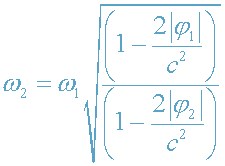 , (27)
, (27)
Таким образом,
частота фотона уменьшается при выходе из поля тяготения
и увеличивается при движении к центру. Если фотон испускается с поверхности
звезды, то r
1=R и |φ
1|=GM/R. В этом случае в приближении слабого поля (14)
формула (27) принимает вид
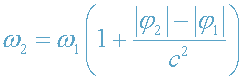 ,
,
что совпадает с формулой (15) задачи 2.
2. Энергия частицы в ОТО.
При движении частицы в постоянном поле тяготения
сохраняется ее полная энергия
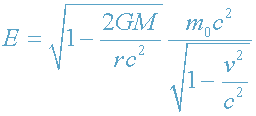 , (28)
, (28)
где m
0 - масса покоя частицы, v - ее
физическая скорость, - это скорость,
измеренная в собственном времени τ, т.е. наблюдателем, находящемся в данном
месте [4.-C.325]. Соответственно, полная энергия фотона в поле тяготения
теперь определяется формулой
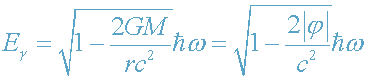 , (29)
, (29)
где ω - частота фотона, измеренная в собственном времени τ.
Из закона сохранения энергии фотона
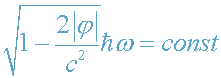 (30)
(30)
опять получаем соотношение (27).
Очевидно, что в предельном случае слабого поля (14) формула (29)
принимает классический вид
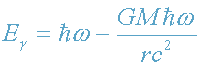
(см. задачу 2).
3. Скорость фотона в ОТО.
В задаче 2 скорость фотона в поле тяготения звезды
определялась классической формулой
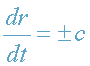
.
В ОТО движение фотона вдоль радиального направления Or определяется уравнением
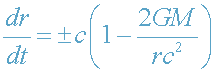 (31)
(31)
где dr/dt - скорость изменения координаты r с течением времени t далекого
наблюдателя (а не физического времени τ в данной точке), т.е. dr/dt -
это
координатная, а не физическая скорость. Физическая скорость есть изменение
физического радиального расстояния
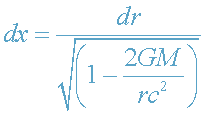 (32)
с физическим временем
(32)
с физическим временем
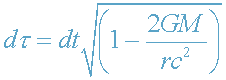 (33)
(33)
(cм. (25)), т.е.
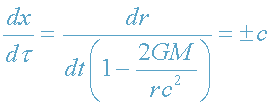 (34)
Физическая скорость фотона в любой системе отсчета равна с!
(34)
Физическая скорость фотона в любой системе отсчета равна с!
Множители
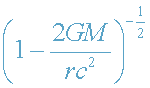
и
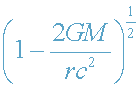
, входящие в формулы (32)-(33), описывают
искривленность пространства-времени! В предельном случае слабого поля (14),
или когда GM/rc
2->0, искривленное пространство-время Эйнштейна-Шварцшильда
переходит в плоское пространство-время Минковского! В этом случае dτ=dt,
dx=dr и, следовательно, координатная скорость фотона (31) совпадает с его
физической скоростью (34).
4. О замедлении времени и распространении света в поле черной
дыры Шварцшильда.
До сих пор мы обсуждали эффекты слабого гравитационного поля,
когда выполняется условие (14). Теперь рассмотрим эффекты сильного
гравитационного поля, в котором
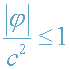
.
Наиболее яркими представителями небесных тел, создающими такие сильные поля, являются
черные дыры, вблизи которых искривление пространства-времени становится очень сильным.
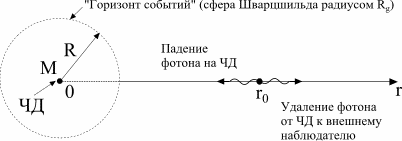
Рис.3. |
Черная дыра Шварцшильда создает в пространстве сферически-симметричное
гравитационное поле (такие черные дыры не вращаются и не имеют электрического
заряда). Никакое излучение, никакие частицы не выходят к внешнему наблюдателю
из под сферы Шварцшильда. Только из точек с r=r0>Rg
частицы и фотоны могут уйти к внешнему наблюдателю.
|
Как известно, черная дыра ЧД - это область пространства-времени, в которой
гравитационное поле настолько сильно, что даже свет не может покинуть эту
область. Граница, отделяющая эту область пространства-времени от окружающего
мира, называется горизонтом событий (см.рис.З): все, что происходит внутри
горизонта событий, скрыто от глаз внешнего наблюдателя [4]
(популярное изложение физики черных дыр см. в [5-7]).
Как мы уже знаем из
задачи 4 (и комментария 1.), темп течения времени тем медленнее, чем ближе
часы к гравитирующему телу. Такое замедление времени проявляется для внешнего
наблюдателя в "покраснении" фотонов, испущенных источником, находящимся
вблизи гравитирующего тела (гравитационное красное смещение, - см. задачу 2
и комментарий 2). А как изменится темп течения времени, если приближаться к
гравитационному радиусу (сфере Шварцшильда) ЧД? Из соотношения (25) следует,
что
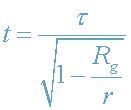 .
.
Как видим, при r->R
g 
,
т.е.
время с точки зрения далекого наблюдателя вблизи
Rg вообще останавливается ("застывает")!
Как сильно "покраснеют" фотоны, испущенные вблизи сферы Шварцшильда с точки
зрения внешнего наблюдателя? Пусть фотон частоты ω
0 испущен из точки
r
0>R
g, в которой потенциал поля φ
0=-GM/r
0 (рис.3).
Тогда в точке r>r
0 наблюдатель зафиксирует фотон частоты (см.(27))
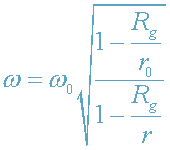 .
.
Как видим, при r
0->R
g ω->0 ,
а при r
0=R
g ω=0, т.е.
где бы ни находился внешний
наблюдатель, ЧД для него в принципе визуально ненаблюдаема!
Рассмотрим подробнее движение фотона вдоль радиальной линии Or в поле
тяготения ЧД Шварцшильда (рис.3).
С точки зрения далекого наблюдателя изменение физического радиального
расстояния dx (см.(32)) с течением времени dt (см.(33)) есть
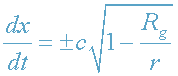 .
.
Как видим, для далекого наблюдателя фотон вблизи R
g движется медленнее,
и при r
0->R
g dx/dt->0!
Очевидно, что это отражает замедление времени вблизи R
g, о чем уже
было сказано выше. Еще раз заметим, что физическая скорость фотона всегда
равна с:
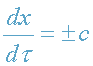
(см.(34)).
Сколько времени по часам далекого наблюдателя понадобится фотону, чтобы,
двигаясь по радиусу от точки r
0, достигнуть произвольной точки r (рис.З)?
Для ответа на этот вопрос перепишем уравнение (31) в виде
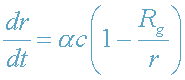 . (35)
. (35)
где α=+1 при r>r
0 - удаление фотона от ЧД,
α=-1 при r<r
0 - "падение" фотона на ЧД.
Элементарное интегрирование уравнения (35) дает результат
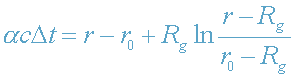 .
.
Таким образом, окончательно получаем:
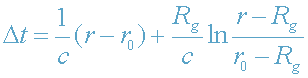 при α=+1; (36)
при α=+1; (36)
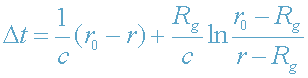 при α=-1; (37)
при α=-1; (37)
Из (36) следует, что при r
0->R
g

,
т.е.
для внешнего наблюдателя ЧД является "застывшим" телом, которое не посылает в
окружающее пространство никаких сигналов и взаимодействует с внешним миром только
своим статическим гравитационным полем. Из (37) следует, что при r->R
g

, т.е.
с какого бы
расстояния ни начинал свое падение фотон, по часам далекого наблюдателя
время достижения фотоном сферы Шварцшильда бесконечно; при r->Rg
все процессы на сфере Шварцшильда по отношению к внешнему наблюдателю "застывают"!
Как видим, относительность времени, т.е. зависимость темпа хода часов от
системы отсчета, проявляется вблизи ЧД особенно ярко.
В заключение, возвращаясь к слабым полям, рассмотрим следующий пример:
из (36) вычислим время, за которое свет проходит расстояние от Солнца до
Земли. Мы уже знаем, что для Солнца
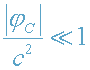
(см. задачи 2, 3). Кроме того, R
g=2GM
C/c
2=3 км,
т.е. R
g<<R
C=7,0*10
8 м.
При r=α=1,5*10
11 и r
0=R
C из (36) получаем:
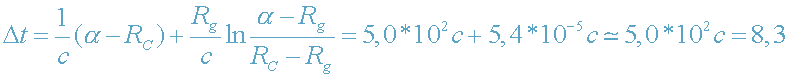
мин.
По существу имеем классический результат
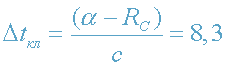
мин.,
т.к. поле тяготения "обычной" звезды является ньютоновским и, следовательно,
релятивистская поправка к
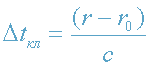
в формуле (36) является очень малой, т.е.
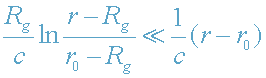
.
Литература.
- А.Т.Глазунов и др. Физика: учебное пособие для 11 класса школ и классов с углубленным
изучением физики. Под ред. А.А.Пинского. - М.; Просвещение. 1994.
- А.В,Засов, Э.В.Кононович. Астрономия: Учебник для 11 класса школ и классов с
углубленным изучением физики и астрономии. - М.: Просвещение. 1993.
- Е.П.Левитан. Астрономия: Учебник для 11 класса общеобразовательных учреждений. -
М.: Просвещение. 1994.
- Л.Д.Ландау, Е.М.Лифшиц. Теория поля. - М.: Наука. 1988.
- В.Б.Брагинский. А.Г.Полнарев. Удивительная гравитация. - М.: Наука. 1985.
- Дж.Нарликар. Гравитация без формул. - М.: Мир. 1985.
- Энциклопедия для детей. Т. 8. Астрономия. - М.: Аванта+. 1997.


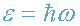 и потенциальной энергии ЕПОТ,
есть величина постоянная, т.е.
и потенциальной энергии ЕПОТ,
есть величина постоянная, т.е.
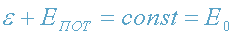 , (1)
, (1)
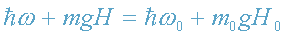 . (2)
. (2)
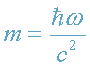 , то из (2) получаем:
, то из (2) получаем:
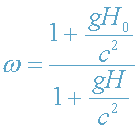 . (3)
. (3)
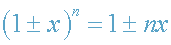 при x<<1 и пренебрегая величинами второго порядка малости
(gH0*gH/c4->0), формулу (3) приводим к виду
при x<<1 и пренебрегая величинами второго порядка малости
(gH0*gH/c4->0), формулу (3) приводим к виду
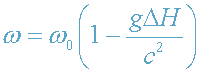 , (4)
, (4)
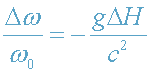 . (5)
. (5)
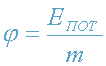 . (6)
. (6)
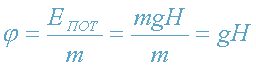 . (7)
. (7)
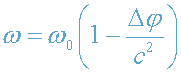 ,
,
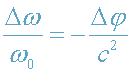 , (8)
, (8)
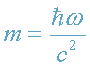 . Запишем уравнение движения частицы с переменной массой:
. Запишем уравнение движения частицы с переменной массой:
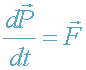 , где
, где 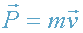 - импульс частицы, движущейся в поле силы
- импульс частицы, движущейся в поле силы 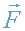 [1-c.237].
При
[1-c.237].
При 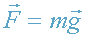 , где
, где 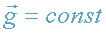 (постоянное однородное поле тяготения), имеем:
(постоянное однородное поле тяготения), имеем:
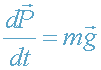 ,
или в проекциях на ось координат ОХ (рис.1)
,
или в проекциях на ось координат ОХ (рис.1)
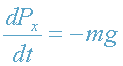 . (9)
. (9)
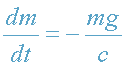 . Разделяя переменные m и t, запишем:
. Разделяя переменные m и t, запишем:
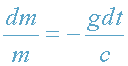 . Т.к. масса фотона
. Т.к. масса фотона
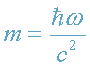 и dx=cdt, то последнее уравнение приводим к виду
и dx=cdt, то последнее уравнение приводим к виду
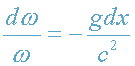 . Интегрируя, получаем:
. Интегрируя, получаем:
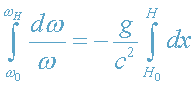 ,
,
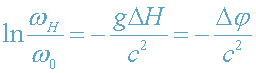 ,
,
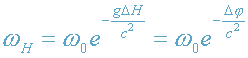 . (10)
. (10)
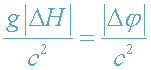 , формулу (10) приводим к виду (4) (или (8)).
При этом надо учесть, что
, формулу (10) приводим к виду (4) (или (8)).
При этом надо учесть, что 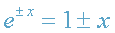 при х<<1.
при х<<1.

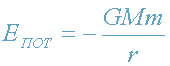 ,
где
,
где 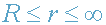 (потенциальная энергия "нормирована на
ноль" в бесконечности). Соответственно, потенциал поля (6) в данной точке
пространства определяется формулой
(потенциальная энергия "нормирована на
ноль" в бесконечности). Соответственно, потенциал поля (6) в данной точке
пространства определяется формулой 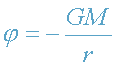 .
Очевидно, что EПОТ=mφ. Закон
сохранения энергии фотона (1) запишем в виде
.
Очевидно, что EПОТ=mφ. Закон
сохранения энергии фотона (1) запишем в виде
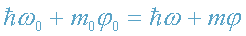 . (11)
. (11)
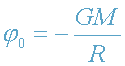 - потенциал поля на поверхности звезды
(в месте испускания фотона),
- потенциал поля на поверхности звезды
(в месте испускания фотона),
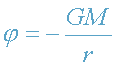 - потенциал поля на расстоянии r от центра звезды
(в месте наблюдения фотона). Учитывая, что масса фотона
- потенциал поля на расстоянии r от центра звезды
(в месте наблюдения фотона). Учитывая, что масса фотона 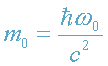 (в месте испускания) и
(в месте испускания) и 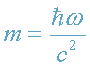 (в месте наблюдения),
уравнение (11) перепишем в виде
(в месте наблюдения),
уравнение (11) перепишем в виде
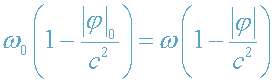 , (12)
, (12)
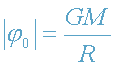 и
и 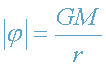 .
Из (12) получаем:
.
Из (12) получаем:
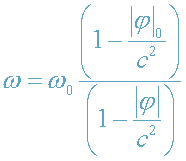 . (13)
. (13)
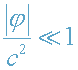 , (14)
, (14)
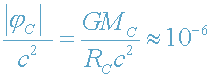 .
В приближении слабого поля (14) формулу (13) приводим к виду
.
В приближении слабого поля (14) формулу (13) приводим к виду
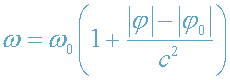 , (15)
, (15)
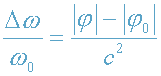 . (16)
. (16)
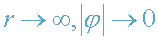 )
формулы (15) - (16) принимают вид:
)
формулы (15) - (16) принимают вид:
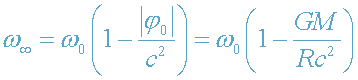 , (17)
, (17)
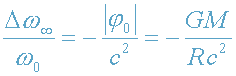 . (18)
. (18)
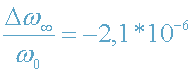 .
.
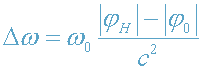 , (19)
, (19)
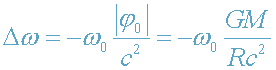 , (20)
, (20)
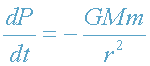 или,
т.к.
или,
т.к. 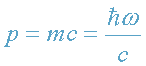 , то
, то
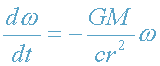 . Умножив обе части этого уравнения на dr=cdt
и разделяя переменные ω и r, получаем:
. Умножив обе части этого уравнения на dr=cdt
и разделяя переменные ω и r, получаем:
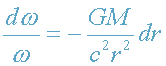 .
.
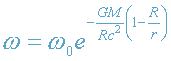 . (21)
. (21)
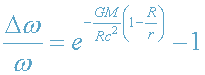 . (22)
. (22)
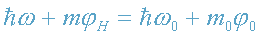 ,
где φ0 и φH - потенциал гравитационного
поля Солнца и Земли в месте испускания и в месте приема фотона соответственно:
,
где φ0 и φH - потенциал гравитационного
поля Солнца и Земли в месте испускания и в месте приема фотона соответственно:
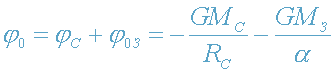 ,
,
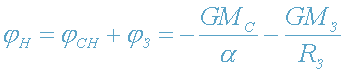
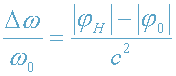 . (23)
. (23)
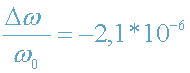 (см. также задачу 2).
Т.к.
(см. также задачу 2).
Т.к. 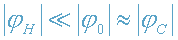 , то для Солнца и тем более для других,
более удаленных звезд, спектры которых наблюдаются на Земле, формулу (23) можно
записать в виде
, то для Солнца и тем более для других,
более удаленных звезд, спектры которых наблюдаются на Земле, формулу (23) можно
записать в виде
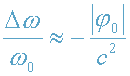
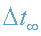 - промежуток
времени между этими же сигналами, регистрируемыми бесконечно удаленным
наблюдателем. Сравнить эти промежутки времени.
- промежуток
времени между этими же сигналами, регистрируемыми бесконечно удаленным
наблюдателем. Сравнить эти промежутки времени.
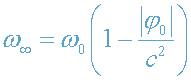 .
.
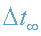 можно подразумевать периоды электромагнитного сигнала:
можно подразумевать периоды электромагнитного сигнала:
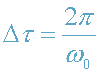 и
и 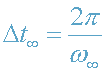 .
Тогда связь между Δτ и Δt имеет вид:
.
Тогда связь между Δτ и Δt имеет вид:
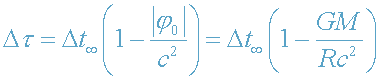 . (24)
. (24)
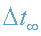 ,
т.е. время на поверхности звезды течет медленнее,
чем для удаленного наблюдателя, причем чем больше абсолютная величина
гравитационного потенциала на поверхности звезды |φ0|, тем медленнее там
течет время!
,
т.е. время на поверхности звезды течет медленнее,
чем для удаленного наблюдателя, причем чем больше абсолютная величина
гравитационного потенциала на поверхности звезды |φ0|, тем медленнее там
течет время!
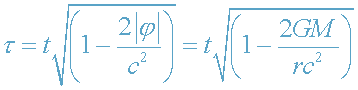 , (25)
, (25)
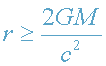 (внешнее решение Шварцшильда).
Радиус
(внешнее решение Шварцшильда).
Радиус 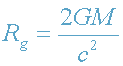 называется радиусом Шварцшильда
или гравитационным радиусом, а сфера с радиусом Rg - сферой
Шварцшильда. Для обычных небесных тел R>>Rg.
называется радиусом Шварцшильда
или гравитационным радиусом, а сфера с радиусом Rg - сферой
Шварцшильда. Для обычных небесных тел R>>Rg.
 )
τ=t, т.е. t - это физическое время наблюдателя на бесконечности. При меньших r время τ течет
все медленнее по сравнению со временем на бесконечности. При r=R
|φ|=|φ0|=GM/R формула (25) принимает вид
)
τ=t, т.е. t - это физическое время наблюдателя на бесконечности. При меньших r время τ течет
все медленнее по сравнению со временем на бесконечности. При r=R
|φ|=|φ0|=GM/R формула (25) принимает вид
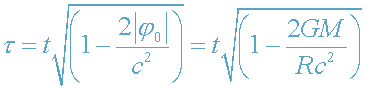 . (26)
. (26)
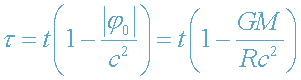 ,
,
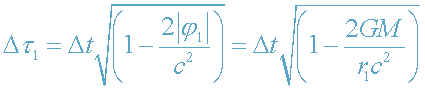 ,
,
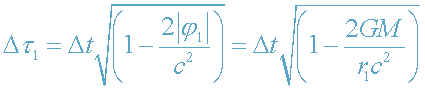 .
.
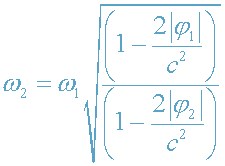 , (27)
, (27)
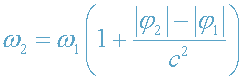 ,
,
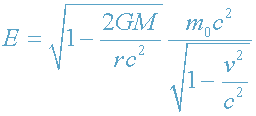 , (28)
, (28)
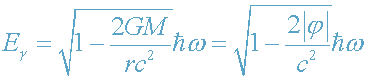 , (29)
, (29)
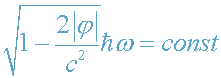 (30)
(30)
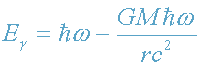
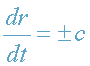 .
В ОТО движение фотона вдоль радиального направления Or определяется уравнением
.
В ОТО движение фотона вдоль радиального направления Or определяется уравнением
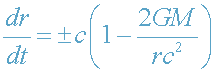 (31)
(31)
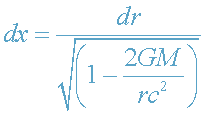 (32)
(32)
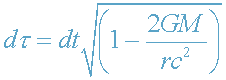 (33)
(33)
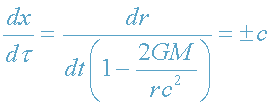 (34)
(34)
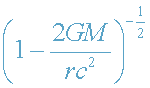 и
и
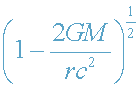 , входящие в формулы (32)-(33), описывают
искривленность пространства-времени! В предельном случае слабого поля (14),
или когда GM/rc2->0, искривленное пространство-время Эйнштейна-Шварцшильда
переходит в плоское пространство-время Минковского! В этом случае dτ=dt,
dx=dr и, следовательно, координатная скорость фотона (31) совпадает с его
физической скоростью (34).
, входящие в формулы (32)-(33), описывают
искривленность пространства-времени! В предельном случае слабого поля (14),
или когда GM/rc2->0, искривленное пространство-время Эйнштейна-Шварцшильда
переходит в плоское пространство-время Минковского! В этом случае dτ=dt,
dx=dr и, следовательно, координатная скорость фотона (31) совпадает с его
физической скоростью (34).
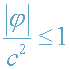 .
Наиболее яркими представителями небесных тел, создающими такие сильные поля, являются
черные дыры, вблизи которых искривление пространства-времени становится очень сильным.
.
Наиболее яркими представителями небесных тел, создающими такие сильные поля, являются
черные дыры, вблизи которых искривление пространства-времени становится очень сильным.

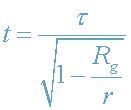 .
.
 ,
т.е. время с точки зрения далекого наблюдателя вблизи
Rg вообще останавливается ("застывает")!
,
т.е. время с точки зрения далекого наблюдателя вблизи
Rg вообще останавливается ("застывает")!
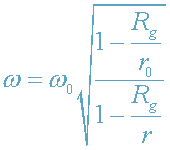 .
.
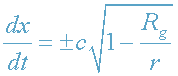 .
.
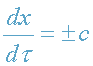 (см.(34)).
(см.(34)).
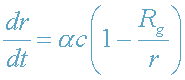 . (35)
. (35)
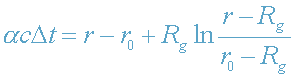 .
.
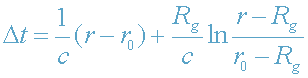 при α=+1; (36)
при α=+1; (36)
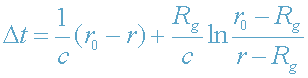 при α=-1; (37)
при α=-1; (37)
 ,
т.е. для внешнего наблюдателя ЧД является "застывшим" телом, которое не посылает в
окружающее пространство никаких сигналов и взаимодействует с внешним миром только
своим статическим гравитационным полем. Из (37) следует, что при r->Rg
,
т.е. для внешнего наблюдателя ЧД является "застывшим" телом, которое не посылает в
окружающее пространство никаких сигналов и взаимодействует с внешним миром только
своим статическим гравитационным полем. Из (37) следует, что при r->Rg
 , т.е. с какого бы
расстояния ни начинал свое падение фотон, по часам далекого наблюдателя
время достижения фотоном сферы Шварцшильда бесконечно; при r->Rg
все процессы на сфере Шварцшильда по отношению к внешнему наблюдателю "застывают"!
, т.е. с какого бы
расстояния ни начинал свое падение фотон, по часам далекого наблюдателя
время достижения фотоном сферы Шварцшильда бесконечно; при r->Rg
все процессы на сфере Шварцшильда по отношению к внешнему наблюдателю "застывают"!
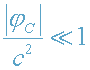 (см. задачи 2, 3). Кроме того, Rg=2GMC/c2=3 км,
т.е. Rg<<RC=7,0*108 м.
При r=α=1,5*1011 и r0=RC из (36) получаем:
(см. задачи 2, 3). Кроме того, Rg=2GMC/c2=3 км,
т.е. Rg<<RC=7,0*108 м.
При r=α=1,5*1011 и r0=RC из (36) получаем:
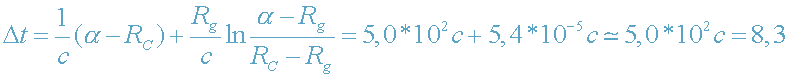 мин.
мин.
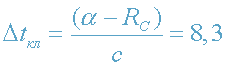 мин.,
т.к. поле тяготения "обычной" звезды является ньютоновским и, следовательно,
релятивистская поправка к
мин.,
т.к. поле тяготения "обычной" звезды является ньютоновским и, следовательно,
релятивистская поправка к 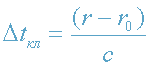 в формуле (36) является очень малой, т.е.
в формуле (36) является очень малой, т.е. 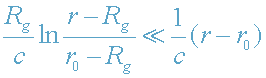 .
.